The "Birthday Problem" simulated with Python

A few days ago I found myself having a vague recollection of an interesting statistics problem. All I could remember was that it had to do with having a room full of people and the probability that any two people in that room would have the same birthday. I remembered the point, which was that it is much more likely than you might think, but I was fuzzy on the details.

After trying to define the problem and find an answer mathematically, I remembered that I suck at statistical reasoning about as much as the average person. So I decided to model the problem with a short Python script and find the answer that way.

Sure, I could've looked it up, but where's the fun in that?

The problem: There are n people (say, at a party) drawn randomly from a population in which the chances of having a birthday on any day is equal to having a birthday on any other (which is not true of real populations (probably)). What is the probability of there being at least two people with the same birthday in the sample?

To put this thing together, I figure we need three things:

1. The ability to generate random numbers (provided by Python's random module);
2. An object representing each person;
3. A "Party" object full of those people.

Then we can add things like the ability to choose how many people we want at the party and how many parties to have, as well as some output for making plots!

import random
random.seed()

# First, the `Person` object. All each person needs is a birthday.

class Person:
    def __init__( self ):
        self.birthday = random.randint( 1, 365 )

# After that we need a Party object, which must be able to
# contain a bunch of people and check to see whether any
# of them have the same birthday.

class Party:
    def __init__( self, partiers ):
        self.members   = [ Person() for p in range(partiers) ]
        self.birthdays = [ member.birthday for member in self.members ]
        self.check_matching_birthdays()

    def check_matching_birthdays( self ):
        birthday_frequencies = { b:0 for b in self.birthdays }
        for b in self.birthdays: birthday_frequencies[b] += 1
        for b in self.birthdays:
            if birthday_frequencies[b] < 2:
                del birthday_frequencies[b]
        self.matching_dates = len(birthday_frequencies)

# Finally, we need the _**main()**_ function
# allowing the user to choose the number of parties and attendees.

def main():
    while True:
        parties  = int(input("Number of parties:  "))
        partiers = int(input("Number of partiers: "))
        parties_with_matching_birthdays = 0

        for party in range( parties ):
            party = Party( partiers )
            if party.matching_dates:
                parties_with_matching_birthdays += 1

        print( 'Fraction of parties having at least one match:' )
        print( '   ', parties_with_matching_birthdays / parties )

main()

Putting it all together we get a tiny program that allows you to answer the question given, and for any number of people. As you increase the number of parties, the variability gets smaller and smaller (and, being an inefficient program, the time taken gets longer and longer).

Here's the output I get from running 10,000 party simulations for each of a few numbers of attendees:

Partiers	Mutual birthday frequency
20	0.4132
25	0.5567
30	0.6999
40	0.8897
50	0.9719

At 25 people there is already a better-than-even chance of finding two people with the same birthday, and by 50 it's almost guaranteed! That does seem a little unbelievable, so I'll refer you to the Wikipedia page on the topic for the math.

Just to see if this little simulation would recreate what Wikipedia shows, we can modify the main() function and change it to the following:

def main():
    max_partiers      = 60
    number_of_parties = 10000
    iterations        = 3

    with open( 'birthdays.r', 'w' ) as rfile:
        # First add the variable containing each number of people.
        rfile.write( 'people = c( 1' )
        for partier in range( 2, max_partiers+1 ):
            rfile.write( ', ' + str(partier) )
        rfile.write( ')\\n' )

        # Then the variables for the matches in each iteration.
        for iteration in range(iterations):
            rfile.write( 'matches' + str( iteration ) + ' = c( 0' )
            for partiers in range( 2, max_partiers+1 ):
                print( 'iteration =', iteration, 'partiers =', partiers )
                matches = 0
                for party in range( number_of_parties ):
                    party = Party( partiers )
                    if party.matching_dates:
                        matches += 1
                rfile.write( ', ' + str( matches / number_of_parties ) )
            rfile.write( ')\\n' )

Plotting the results in R gives:

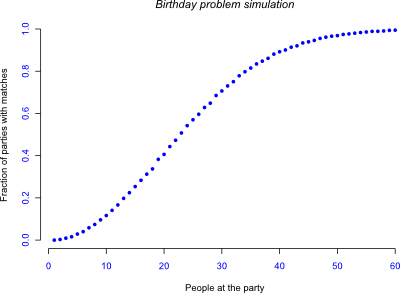
And overlaying it onto the Wikipedia plot: